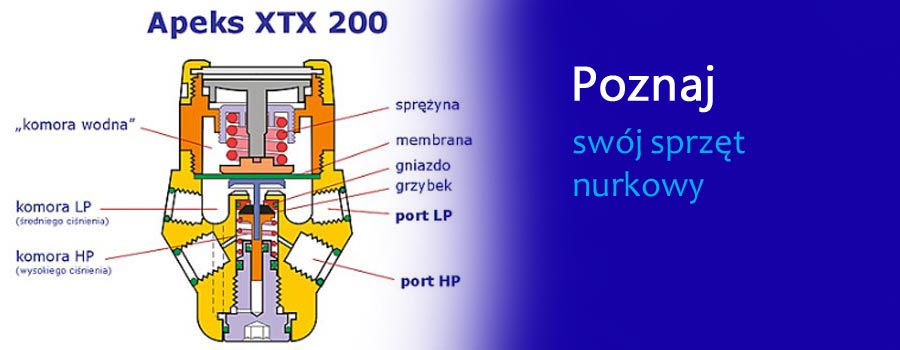
Jak zapisać się na kurs nurkowania!

Kursy nurkowania prowadzimy w Krakowie. Zależy ci na szybkim terminie - skontaktuj się z instruktorem
Tel.: (+48) 501 627 846. lub e-mail. Zawsze możesz zadzwonić i zapytać. Preferujemy kontakt telefoniczny. Więcej.

Wpływ zjawiska Joule'a-Thomsona na zamarzanie automatów

fizyka nurkowania

W wielu książkach szukałem wyjaśnienia tego zagadnienia, materiałów jest sporo, jednak nigdzie nie wyło to wyjaśnione w przypadku konkretnych mieszanek oddechowych. Nurków interesuje jak skład mieszanki oddechowej wpływa na zamarzanie automatów oddechowych. Wyniki w przypadku mieszanek z dodatkiem helu są bardzo ciekawe.

Generalnie dodanie helu do mieszanki oddechowej zmniejsza ryzyko zamarznięcia automatu oddechowego, przez zmniejszenie spadku temperatury gazu w trakcie rozprężania na pierwszym stopniu. Przykładowo podam że zaczynając od mieszanki trimix 16/20 (FO2=0,16; FHe=0,20), zamarzanie nie jest możliwe, przynajmniej w wodzie o temperaturze 5 stopni Celsjusza.
Tlen natomiast jest czynnikiem zwiększającym prawdopodobieństwo zamarznięcia automatu oddechowego (większy spadek temperatury). Nurkowanie pod lodem na mieszankach bogatych w tlen (nitrox) wydaje sie niecelowe.

Poniższy opis pochodzi z strony Podkomisji Nurkowania Jaskiniowego i doskonale ilustruje istotę problemu.

Temperatura mieszanki oddechowej za pierwszym stopniem automatu

Celem niniejszego artykułu jest pokazanie praktycznego sposobu na wyznaczanie temperatury mieszanki oddechowej po rozprężeniu na pierwszym stopniu automatu.

Niepokojące może się jednak wydawać to, że zjawisko to jest owiane pewnym nimbem tajemniczości, który wynika z szeregu niedomówień. Nie należy tego zjawiska demonizować, trzeba natomiast dokładnie i prosto wyjaśnić jego termodynamiczne podstawy.

Na wstępie przypomnijmy jeszcze raz, kluczową dla zrozumienia zjawiska Joule'a-Thomsona, różnicę pomiędzy gazem doskonałym a rzeczywistym. Cząsteczki gazu idealnego traktujemy jako punkty materialne, które zderzają się między sobą w sposób sprężysty. Ponadto, co najważniejsze, pomiędzy cząsteczkami gazu doskonałego nie zachodzą żadne oddziaływania, to znaczy te cząsteczki ani się nie przyciągają ani nie odpychają. Dla większości przemian termodynamicznych, opis za pomocą gazu doskonałego daje wystarczająco dobre przybliżenie. Niemniej jednak są zjawiska, dla których to nie wystarcza. Do takich zjawisk należy właśnie efekt Joule'a Thomsona.

W gazie rzeczywistym cząsteczek nie można już traktować jak punkty materialne. W zależności od odległości w jakiej się znajdują, dwie cząsteczki gazu mogą się odpychać lub przyciągać. Skąd biorą się takie oddziaływania? Obecność sił odpychających można wyobrazić sobie na podstawie eksperymentu myślowego. Niech cząsteczki gazu będą piłkami tenisowymi. Jeśli worek z takimi piłkami ściśniemy wystarczająco mocno, to zmniejszymy odległości miedzy nimi do tego stopnia, że ich powierzchnie ugną się i piłeczki będą odpychały się. Powstaje siła odpychająca. Te siły są odpowiedzialne za obecność energii potencjalnej w gazie.

Otóż jeżeli sprężamy (adiabatycznie) gaz doskonały, to cała energia przekazana w tym procesie do gazu przechodzi w energie kinetyczną cząsteczek (związaną z ruchem), co odczuwamy jako wzrost temperatury. Natomiast jeżeli sprężamy gaz rzeczywisty, to tylko pewna część energii zostanie przekazana na zwiększenie prędkości ruchu cząsteczek. Pozostała energia zostanie zużyta na ugięcie "powierzchni piłeczek". Tak więc energia zgromadzona w gazie rzeczywistym składa się z energii kinetycznej i potencjalnej cząsteczek.

Przyciąganie się cząsteczek w gazie rzeczywistym jest może mniej oczywiste. Atomy gazu należy rozumieć jako chmury ujemnie naładowanych elektronów otaczających małe dodatnie jądra. Rozkład ładunku elektrycznego w powłoce elektronowej nie jest równomierny. Powoduje to polaryzację atomów, a co za tym idzie ich wzajemne przyciąganie.

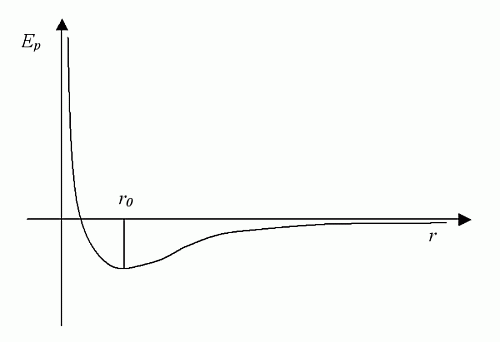
Rys. 1. Krzywa Lennarda-Jonesa.

W zależności od tego w jakiej odległości od siebie są cząsteczki gazu, przeważa albo odpychanie albo przyciąganie. Jeżeli cząsteczki są blisko siebie (co dopowiada dużym ciśnieniom) to przeważa odpychanie. Natomiast jeżeli cząsteczki są daleko od siebie (niskie ciśnienia) to przeważa przyciąganie. Tę zależność opisuje krzywa Lennarda-Jonesa pokazana na rysunku 1. Na osi poziomej podano odległość między cząsteczkami. Na osi pionowej pokazano wartość energii potencjalnej, którą posiadają cząsteczki znajdujące się w odległości r. Oznacza to, że jeśli zbliżymy do siebie cząsteczki, to wtedy zaczynają się gwałtownie odpychać. W większej odległości cząsteczki mają już na tyle miejsca, że się już nie odpychają. Do głosu zaczynają dochodzić przyciągające siły elektryczne. Energia potencjalna staje się ujemna. Gdy cząsteczki odsuniemy od siebie do nieskończoności, to jakiekolwiek oddziaływania miedzy nimi zanikną do zera.

Uzbrojeni w tę wiedzę możemy przeanalizować zjawiska zachodzące w gazie przepływającym przez I stopień automatu (rysunek 2). Podstawą do analizy jest wykonanie bilansu energii, ciepła i pracy w obszarze obejmującym zawór. Do tego obszaru dopływa gaz o temperaturze T0 i ciśnieniu p0. Zawór pierwszego stopnia jest z punktu widzenia mechaniki płynów przeszkodą miejscową, w której następuje spadek ciśnienia do wartości p1. Interesuje nas to, co się będzie działo z temperaturą T1.

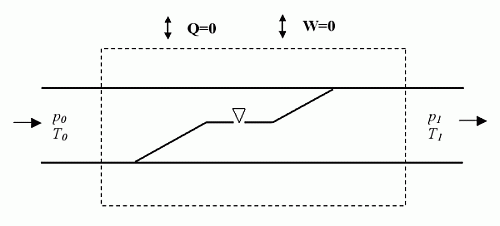
Rys. 2. Schemat przepływu gazu przez zawór w pierwszym stopniu automatu.
Linią przerywaną oznaczono obszar bilansowy.

Przepływ gazu przez zawór jest na tyle szybki, że nie zachodzi w tym czasie wymiana ciepła z otoczeniem. Ponadto przepływający gaz nie wykonuje żadnej pracy, ani też siły zewnętrzne nie wykonują żadnej pracy nad gazem. Zatem energia dostarczona z dopływającym gazem do omawianego obszaru musi być równa energii wyprowadzanej z wypływającym gazem. Energia doprowadzana z przepływającym gazem nosi nawę: entalpia (patrz Magazyn Nurkowanie 62, 12/2000). Mamy tu do czynienia z procesem, w którym entalpia jest stała. Wobec tego nazywa się go dławieniem izentalpowym.

Przeanalizujemy teraz jak przebiega przemiana izentalpowa. Ciśnienie spadło z wartości p0 do wartości p1, co spowodowało wzrost odległości między cząsteczkami gazu. Energia (entalpia) gazu przed i po rozprężeniu musi być taka sama. W gazie doskonałym nie ma energii potencjalnej, czyli cała energia jest zawarta w energii kinetycznej cząsteczek. W tym procesie nie może ona ulec zmianie, czyli efekt Joule'a-Thomsona dla gazu doskonałego jest zerowy.

Natomiast w gazie rzeczywistym wraz ze zmianą odległości cząsteczek zachodzi zmiana energii potencjalnej. Ponieważ sumaryczna energia musi być stała, więc zmiana energii potencjalnej musi być skompensowana zmianą energii kinetycznej - co odczujemy jako zmianę temperatury. Ten fakt stanowi kwintesencję efektu Joule'a Thomsona. Jeżeli gaz przed rozprężeniem znajduje się na prawo od punktu r0, to w wyniku rozprężenia jego energia potencjalna wzrasta, zatem jego energia kinetyczna musi zmaleć, co spowoduje spadek temperatury gazu. Takie zjawisko obserwujemy dla powietrza. Przeciwna sytuacja ma miejsce dla helu.

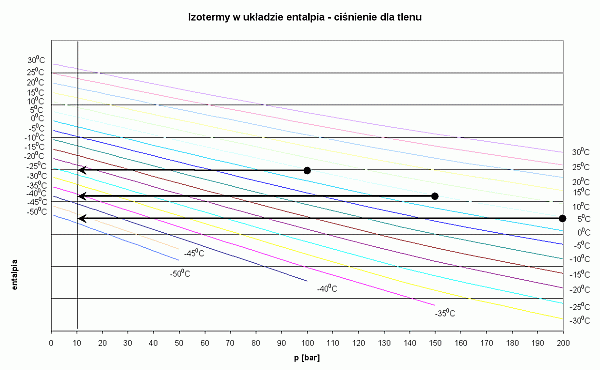
W praktyce nurkowej interesujące jest określenie temperatury, którą osiągnie gaz po przepłynięciu przez pierwszy stopień automatu. Entalpia właściwa jest termodynamiczną zmienną stanu. Efekt Joule'aThomsona można analizować na wykresie entalpia-ciśnienie, na którym naniesiono izotermy odpowiadające interesującym nas temperaturom. Poniżej zamieszczono takie wykresy dla kilku czynników oddechowych. Wykresy te zostały wygenerowane za pomocą obliczeń termodynamicznych w programie PROMIX v 1.02a.

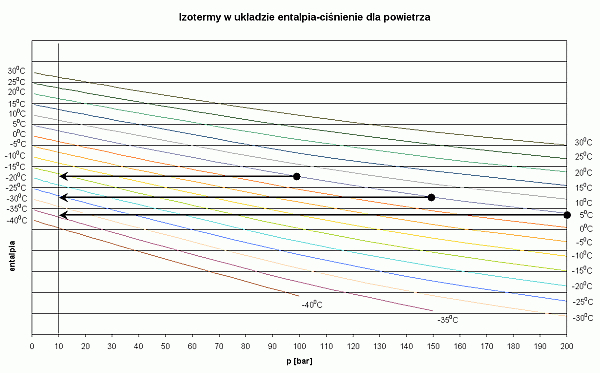
Osoby, które nie chcą wnikać w termodynamiczną istotę procesu, mogą się skoncentrować tylko na mnemotechnicznym wykorzystaniu tych wykresów. Na każdym z nich pokazano za pomocą czarnych strzałek sposób odczytywania temperatury gazu po zdławieniu izentalpowym. Weźmy dla przykładu powietrze. Nurkujemy w wodzie o temperaturze 5 st.C. Wyszukujemy izotermę o tej temperaturze. Ciśnienie początkowe w butli wynosi 200 bar. Na izotermie 5 st.C wyszukujemy punkt, w którym przecina się ona z wartością 200 bar. To miejsce jest zaznaczone czarną kropką. Jest to punkt, w którym zaczyna się przemiana gazu. Ponieważ przemiana jest izentalpowa, to na tym wykresie będzie odbywała wzdłuż linii poziomej. Przemiana kończy się w momencie, gdy osiągniemy ciśnienie końcowe - w tym przypadku 10 bar. Końcowy punkt, zaznaczony strzałką, znajduje się pomiędzy izotermami -30 st.C i -35 st.C. Można przyjąć, że temperatura końcowa będzie wynosiła -34 st.C. Podobna analizę można przeprowadzić, gdy ciśnienie w butli będzie odpowiednio 150 bar i 100 bar. Temperatura powietrza po rozprężeniu będzie wówczas wynosiła odpowiednio -25 st.C oraz -15 st.C.

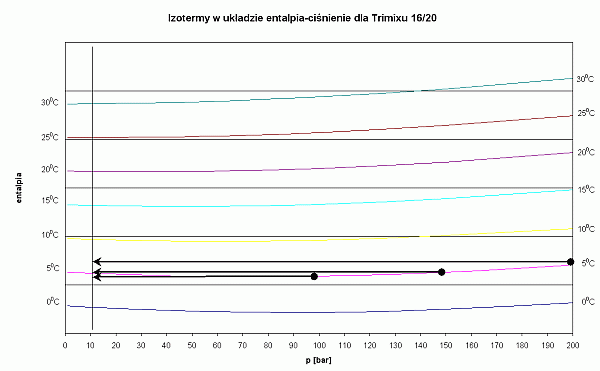
Natomiast jeśli weźmie się pod uwagę trimix 16/20, to okaże się, że izotermy są prawie poziome. W tej mieszaninie prawie wcale nie następuje zmiana temperatury przy przepływie przez pierwszy stopień.

Analizując w podobny sposób pozostałe wykresy można wyciągnąć następujące wnioski:

Im wyższe jest ciśnienie początkowe powietrza w butli, tym niższa jest jego temperatura po rozprężeniu.
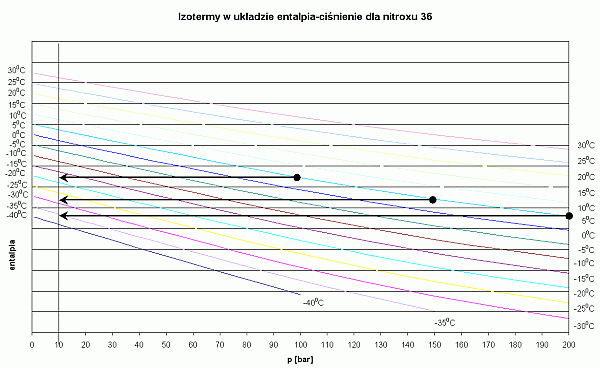
Izotermy dla nitroxu są bardziej strome, zatem przy tych samych warunkach otrzymuje się niższe temperatury po rozprężeniu niż dla powietrza.
Zwiększanie ilości tlenu w mieszance oddechowej powoduje zwiększenie efektu Joule'a Thomsona.
Dekompresja na tlenie podczas nurkowania podlodowego może się łatwo zakończyć zamarznięciem automatu.
Użycie nitroxu przy nurkowaniu podlodowym powoduje, że automat jest bardziej podatny na zamarzanie
Stosując trimix 16/20 nie ma możliwości zamarznięcia automatu, niezależnie od temperatury wody i ciśnienia w butli - izotermy są prawie poziome
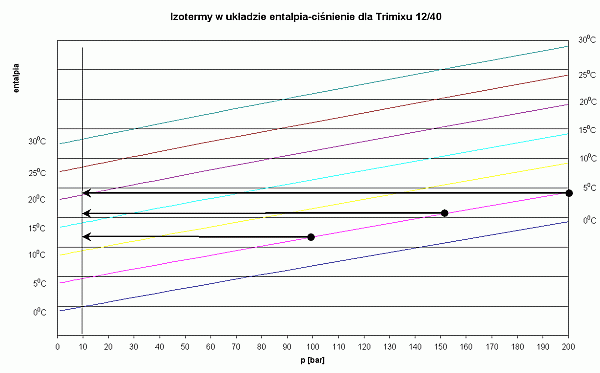
Dla trimixu 12/40 izotermy są nachylone przeciwnie niż dla powierza, temperatura mieszanki po przepłynięciu przez pierwszy stopień zwiększa się.

Poniżej przedstawione są wykresy entalpia-ciśnienie dla kilku różnych gazów używanych w nurkowaniu.